Lo studio degli autovettori e dei corrispondenti autovalori è un qualcosa in cui ci siamo cimentati probabilmente tutti almeno una volta nella vita. In pochi, tuttavia, sanno che questo strumento è di importanza vitale sia per la Social Network Analysis che per la Fisica Quantistica. Nel primo caso, per via di tutto ciò che concerne la centralità.

Senza la pretesa di fornire una trattazione rigorosa sull’argomento come se dovessimo preparare un esame di algebra lineare, qui ci concentreremo sull’intuizione dei concetti fondamentali così da avere tutti le conoscenze necessarie per utilizzarli in ambito di analisi delle reti sociali.

Autovettori e autovalori: una definizione informale

Supponiamo di avere una matrice di trasformazione quadrata \( A \). Essa può essere vista come un operatore perché può essere applicata (mediante prodotto scalare) a un vettore \( \vec{x} \) al fine di ottenere un vettore \( \vec{y} \), ovvero:

\[A\vec{x} = \vec{y}\]

Per chi non ha paura di fare indigestione di algebra lineare possiamo aggiungere che la matrice \( A \) è un endomorfismo.

Ebbene, gli autovettori sono quei vettori che giacciono su delle direzioni caratteristiche della trasformazione \( A \) tali per cui quando sono moltiplicati per \(A \) danno come risultato altrettanti vettori non nulli che si differenziano dai vettori di partenza al più per il modulo e per il verso, mentre le loro direzioni restano invariate.

In altri termini, supponendo che \( A \) sia una matrice \( 2 \times 2 \) di righe linearmente indipendenti, ovvero un endomorfismo in \( \mathbb{R}^2 \), allora esiste qualche coppia \( (x, y) \ne (0, 0) \) che, trasformata mediante \( A \), dia come risultato ancora la coppia \( (x, y) \) moltiplicata per \( \lambda \), che ne modifica il modulo e, eventualmente, il verso ovvero:

\[A(x, y) = \lambda(x, y)\]

I rispettivi coefficienti \( \lambda \) degli autovettori prendono il nome di autovalori. In caso di \( \lambda \) positivo, il rispettivo vettore trasformato non subisce un cambiamento di verso; quando negativo, il verso ne risulterà opposto. Ma, sia come sia, la direzione individuata dagli autovettori non cambia.

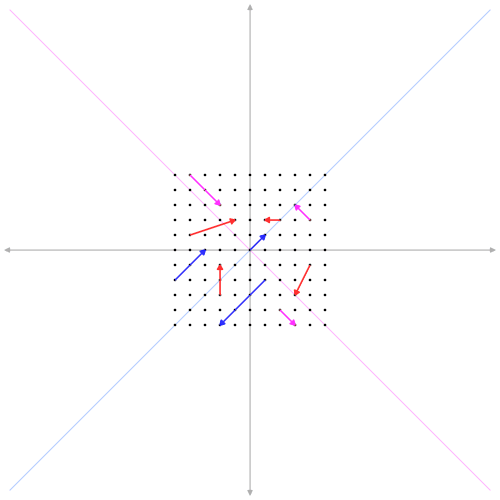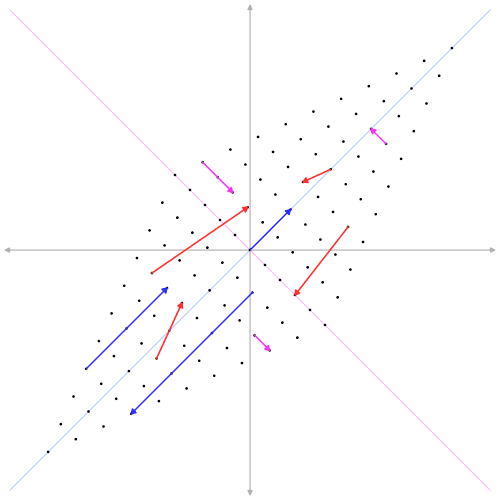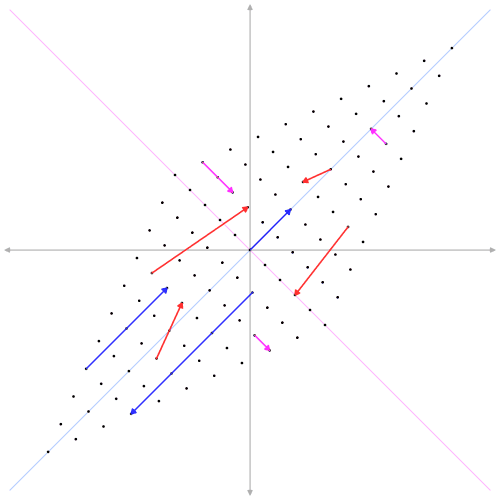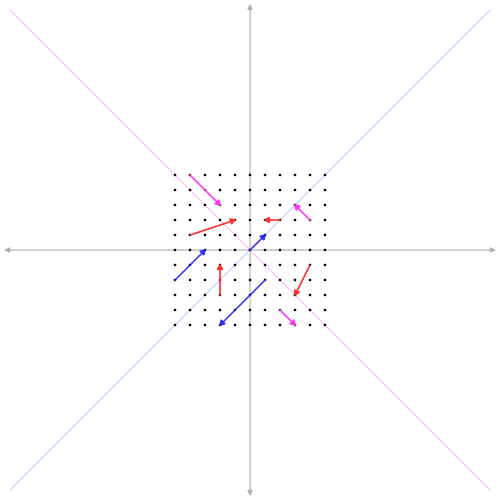
Come calcolare gli autovettori e gli autovalori

Per il calcolo degli autovalori, e quindi degli autovettori, procediamo algebricamente a partire da:

\[A\vec{v} = \lambda\vec{v} \tag{1}\]

che equivale a scrivere

\[\vec{v}(A - \lambda I) = 0 \tag{2}\]

La relazione (2) produce un sistema di equazioni lineari omogeneo ovvero privo del termine noto. Il che significa che è possibile trovare soluzioni non nulle del vettore \( \vec{v} \) solo se il determinante della matrice che moltiplica \( \vec{v} \) è zero. In simboli:

\[\bbox[5px,border:1px solid red]{ det(A - \lambda I) = 0 }\]

che, una volta risolto, ci consente di individuare gli autovalori \( \lambda_{1 \cdots N} \) e i corrispettivi autovettori.

Diagonalizzazione e cambio di sistema di riferimento

Come dicevamo, gli autovettori ricoprono un ruolo essenziale in tanti campi del sapere, dalle scienze delle costruzioni alla meccanica quantistica, dall’elettromagnetismo alla teoria dell’informazione, fino allo studio delle reti.

Alla base di tanta importanza è soprattutto la proprietà degli autovettori di poter trasformare una matrice \( A \) nella sua corrispettiva diagonalizzata, a seguito di un cambio di sistema di riferimento a favore di uno i cui assi siano gli autovettori della matrice stessa. Vediamo praticamente.

Innanzitutto verifichiamo una proprietà molto interessante delle matrici diagonali: quando un vettore \( a \) è moltiplicato per una matrice diagonale \( A \), il vettore risultante \( b \) avrà componenti pari alla proiezione delle componenti del vettore originario sul sistema di assi ortogonali di riferimento moltiplicato scalarmente per i coefficienti sulla diagonale A. Facciamo un esempio.

Supponendo di voler calcolare \( \vec{b} = A\vec{a} \) dati:

\[\vec{a} = \begin{pmatrix} 1 \\\\ 3 \end{pmatrix} A = \begin{bmatrix} 3 & 0 \\\\ 0 & -2 \end{bmatrix}\]

Avremo:

\[\vec{b} = \begin{pmatrix} 1 \\\\ 3 \end{pmatrix} \begin{bmatrix} 3 & 0 \\\\ 0 & -2 \end{bmatrix} = \begin{pmatrix} 3 \\\\ -6 \end{pmatrix}\]

ovvero le componenti \(b_x = 3 \) e \(b_y = -6 \) sono le proiezioni sugli assi \( (x, y) \) del vettore \( \vec{b} \) con un modulo pari alle proiezioni del vettore di partenza \( \vec{a} \) moltiplicati, come abbiamo già detto, per i coefficienti sulla diagonale \( A \).

Questo ragionamento è sorprendentemente simile a quanto abbiamo già detto sugli autovettori, ovvero i vettori caratteristici di una trasformazione che individuano delle direzioni sulle quali giacciono i vettori trasformati modificati al più in modulo e verso da un fattore \( \lambda \)

In altri termini, è possibile rappresentare il vettore \( \vec{a} \) non più con il sistema di assi \( (x, y) \) ma su un nuovo sistema di assi \( (v_1, v_2) \) costruito sulle direzioni degli autovettori della matrice \( A \). Questo vettore trasformato \( \vec{a}’ \) avrà, come sappiamo, componenti di lunghezza pari a quelle del vettore di partenza \( \vec{a} \) moltiplicato per i vari autovalori \( \lambda_N \). In generale queste proiezioni saranno non ortogonali, laddove non lo sia stata la matrice di trasformazione di partenza.

Questo ci consente di affermare due cose.

Innanzitutto ci consente di dire che possiamo utilizzare gli autovettori come assi di riferimento per applicare una trasformazione \( A \) a un vettore \( \vec{a} \), utilizzando gli autovalori \( \lambda_N \) come moltiplicatori delle componenti di \( \vec{a} \) sulle direzioni degli autovettori.

Ma quel che è più importante, ci consente di calcolare le coordinate del vettore \( \vec{a} \) nel nuovo sistema di riferimento individuato dagli autovettori \( (v_1, v_2) \). Vediamo come.

Ricordando che il vettore \( \vec{a} \) è scomponibile nelle due componenti nelle direzioni degli autovettori, supponendo \( \vec{v_1} \) e \( \vec{v_2} \) autovettori normalizzati (cioè con modulo pari a uno), possiamo scrivere questa combinazione lineare:

\[a = \alpha v_1 + \beta v_2\]

che individua un sistema di equazioni lineari che può essere risolto in \( (\alpha, \beta) \) così:

\[\begin{pmatrix} a_x \\\\ a_y \end{pmatrix} = \alpha\begin{pmatrix} v_1x \\\\ v_1y \end{pmatrix} + \beta\begin{pmatrix} v_2x \\\\ v_2y \end{pmatrix} \Rightarrow\] \[\begin{pmatrix} a_x \\\\ a_y \end{pmatrix} = \begin{pmatrix} \alpha v_1x + \beta v_2x \\\\ \alpha v_1y + \beta v_2y \end{pmatrix} \Rightarrow\] \[\begin{pmatrix} a_x \\\\ a_y \end{pmatrix} = \bbox[5px,border:1px solid red]{\begin{pmatrix} v_1x && v_2x \\\\ v_1y && v_2y \end{pmatrix}}\begin{pmatrix} \alpha \\\\ \beta \end{pmatrix}\]

Dove la matrice nel riquadro rosso non è altro che la matrice che ha come colonne le componenti normalizzate degli autovettori della matrice di partenza mentre \( (\alpha, \beta)^T \) è niente altro che la rappresentazione del vettore di partenza \(\vec{a} \) nel nuovo sistema di riferimento dato dagli autovettori.

Se indichiamo la matrice degli autovettori con \( V \) possiamo in definitiva scrivere:

\[\vec{a} = V\begin{pmatrix} \alpha \\\\ \beta \end{pmatrix}\]

ovvero

\[\begin{pmatrix} \alpha \\\\ \beta \end{pmatrix} = V^{-1}A\]

Il nuovo sistema di assi così individuato non sarà necessariamente rappresentato da autovettori ortogonali. Tuttavia, questi potranno essere ortogonalizzati facendoli ruotare relativamente uno agli altri in modo da ottenere variazioni di angoli di, giustappunto, 90°.

L’applicazione più concreta del cambio di assi verso un sistema individuato dagli autovettori è proprio nella diagonalizzazione delle matrici che, come detto, ha diversi vantaggi tra cui la semplificazione dei calcoli. Ebbene, possiamo dimostrare che per diagonalizzare una matrice si possono usare gli autovalori per produrre una base di riferimento ortogonale. Se gli autovettori sono ortogonali, il vettore trasformato manterrà, nel nuovo sistema di riferimento, la stessa lunghezza - e questa è certamente la situazione più auspicabile. In caso contrario, il vettore trasformato presenterà una lunghezza diversa.

Ma vediamo come. Ricordando l’equazione fondamentale degli autovettori per cui in uno spazio a \( N \) dimensioni abbiamo al più \( N \) autovettori e autovalori e la cui espressione del k-esimo è la seguente:

\[A\vec{v_k} = \lambda_k\vec{v_k} \text{ con } k = 1,\ldots,N\]

Ovvero

\[\begin{matrix} A\vec{v_1} = \lambda_1\vec{v_1} \\\\ A\vec{v_2} = \lambda_2\vec{v_2} \\\\ \vdots \\\\ A\vec{v_k} = \lambda_k\vec{v_k} \end{matrix} \Rightarrow\] \[A(v_1 v_2 \ldots v_N) = (v_1 v_2 \ldots v_N)\Lambda\]

con i vettori \( v_k \) gli autovettori e \( \Lambda \) la matrice degli autovalori che, infatti, vale:

\[\Lambda = \begin{pmatrix} \lambda_1 & 0 & \ldots & 0 \\\\ 0 & \lambda_2 & \ldots & 0 \\\\ \vdots & \vdots & \ddots & \vdots \\\\ 0 & 0 & \ldots & \lambda_k \end{pmatrix}\]

che, come si può vedere, è una matrice che presenta sulla diagonale principale i coefficienti degli autovalori della matrice \( A \).

Per finire, andando a indicare con \( V \) la matrice degli autovettori utilizzati precedentemente, otterremo l’equazione fondamentale per la diagonalizzazione di una matrice:

\[\bbox[5px,border:1px solid red]{ VA = V\Lambda }\]

In altri termini, la matrice degli autovalori \( \Lambda \) sarà la rappresentazione diagonale della matrice \( A \) in un sistema di riferimento individuato dagli autovettori di \( A \), o come si dice più propriamente nell’autospazio di \( A \).

Ma a cosa serve tutto ciò?

Una applicazione pratica: la compressione dell’informazione

Sia data una certa matrice quadrata \( A \). La matrice degli autovettori esprime la varianza di \(A \), ovvero le informazioni che contiene. Il quantitativo di varianza espressa da ogni singolo autovettore è espresso dal valore dell’autovettore corrispondente. Vediamolo con un esempio con la seguente matrice \( A \):

\[A = \begin{pmatrix} 2 & -1 & 3 \\\\ 3 & -2 & 2 \\\\ 15 & -9 & 16 \end{pmatrix}\]

(si noti che la matrice A è di ordine 3 con il terzo componente volutamente molto vicino ma non coincidente alla combinazione lineare \( 3a_1 + 3a_2\)).

Ora calcoliamo gli autovalori e gli autovettori corrispondenti:

\[\begin{matrix} \lambda_1 = 17.59 \\\\ \lambda_2 = -1.62 \\\\ \lambda_3 = 0.035 \end{matrix}\] \[V = \begin{pmatrix} -0.18 & 0.26 & -0.64 \\\\ -0.12 & -0.68 & -0.19 \\\\ -0.97 & -0.68 & 0.74 \end{pmatrix}\] \[V^-1 = \begin{pmatrix} -0.81 & 0.47 & -0.93 \\\\ 1.04 & -0.86 & -0.08 \\\\ -0.80 & -0.60 & 0.22 \end{pmatrix}\]

Notiamo subito che \( \lambda_3 \) è molto più piccolo in modulo degli altri due autovalori. Questo significa che il suo contributo all’informazione contenuta in \( A \) è molto ridotto, rispetto agli altri due.

Decidiamo allora di scartarlo e di scartare anche l’autovettore corrispondente.

\[\Lambda = \begin{pmatrix} 17.5 & 0 \\\\ 0 & -1.6 \end{pmatrix}\] \[V = \begin{pmatrix} -0.18 & 0.26 4 \\\\ -0.12 & -0.68 \\\\ -0.97 & -0.68 \end{pmatrix}\] \[V^-1 = \begin{pmatrix} -0.81 & 0.47 & -0.93 \\\\ 1.04 & -0.86 & -0.08 \end{pmatrix}\]

Ora, dalla formula della diagonalizzazione abbiamo che

\[A = V\Lambda V^{-1}\]

e facendo i calcoli abbiamo questa rappresentazione di \( A \) che per distinguerla dall’originaria decoro con un pedice \( R \):

\[A_R = \begin{pmatrix} 1.98 & -1.01 & 3 \\\\ 2.97 & -2.01 & 2 \\\\ 15 & -8.99 & 15.99 \end{pmatrix}\]

che non è identica alla matrice \( A \), ma è senza dubbio estremamente simile ad essa. Ma ottenuta lavorando con matrici di dimensione 2 invece di 3, ovvero con meno calcoli.

Abbiamo, nel concreto, ricostruito la matrice \( A \) utilizzando una sua espressione diagonale valutata su una base di autovettori ridotta rispetto a quella individuabile da \( A \) e nel farlo abbiamo perso un quantitativo trascurabile di informazione.

Geometricamente, abbiamo espresso \( A_R \) in un sistema di riferimento avente un numero di dimensioni più basso rispetto all’ordine di \( A \).

Nella pratica, abbiamo condotto una operazione di compressione dell’informazione.

Autovettori e Social Network Analysis

L’importanza degli autovettori per la scienza dell’informazione, come potete immaginare, già solo per la capacità di ridurre di dimensioni un sistema è estrema. Ma come possiamo applicare questo potente strumento allo studio delle reti sociali?

Per rispondere a questa domanda basta ricordare che noi possiamo sempre esprimere una rete di relazioni attraverso la matrice delle adiacenze. E questa matrice è, tipicamente, non singolare quindi ammette un’inversa e, quindi, su di essa è possibile calcolare gli autovalori e gli autovettori.

Lo vedremo presto su una particolare misura di centralità, chiamata Eigenvector Centrality, sulla quale si è molto parlato negli ultimi anni e ancora di più se ne parlerà in futuro.

E’ la modalità, infatti, su cui Google ha costruito il suo famigerato algoritmo PageRank, per stimare l’autorevolezza e ordinare i link nei risultati del motore di ricerca.

Esatto, Google. E parte tutto da qui.